参考資料−1

水面衝撃荷重について

1. 概要

海面を滑走、或いは半滑走状態で航走する比較的に小型の高速船は、通常船底スラミング荷重によって設計される。実際、長さが50m以下の高速艇においては、船底衝撃水圧に対する局部強度を満足すれば、縦強度は問題ないと言われている。

V型あるいはdeepV型の高速船のスラミング荷重を考える場合、最も簡単なモデルとして2次元の襖形物体の水面衝撃問題として扱うことができる。例えば、V型断面を持つ高速艇が波浪中を運動しながら前進する時、空間に固定された、船体を横切る鉛直な面において、通過する船体の断面と水面の変化を観察すると、船底スラミングは2次元のV断面の物体が水面に突入する状態と似ていることが分かる。2次元の衝撃水圧は後述するように、3次元の衝撃圧の計算にも重要である。初めに2次元の衝撃水圧の計算法と特性について述べる。次に3次元の衝撃水圧の計算法として、Stavovy ＆ Chuangの方法とその修正、応用について述べる。

2. 2次元の衝撃水圧1）

（1）Karmanの理論

2次元の水面衝撃荷重については、これまで多くの研究が行われており、最近、精密な計算法等も提案されているが、von Karman とWagnerの理論は最も基礎的で代表的なものである。vonKarman、Wagner等は飛行艇の着水時の荷重推定法として、2次元の楔形物体の水面衝撃を考えた。

von karmanは、図−1のように楔が水面に突入する時、付加質量の時間変化により力が作用するものとし、水面の変形を無視して水の密度ρと接水幅cを用いて付加質量を（1/2）ρπc2で近似し、楔形物体に働く荷重Pを次式で与えている。

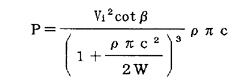
ここに、Wは物体の重量、Viは着水速度である。Pは衝撃荷重であり、衝撃圧の分布はここでは考えていない。

（2）Wagner,Ferdinande2）の理論

これに対しWagnerは図−2に示すように楔の着水による水面の盛り上がりを考慮に入れ、衝撃荷重を導いた。楔形物体の場合には衝撃水圧pは次式で与えられる。

前ページ　　　目次へ　　　次ページ